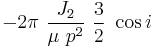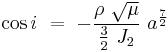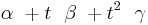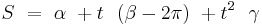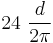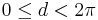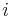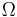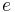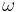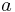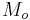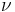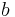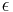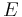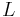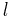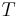Sun-synchronous orbit
A Sun-synchronous orbit (sometimes called a heliosynchronous orbit) is a geocentric orbit which combines altitude and inclination in such a way that an object on that orbit ascends or descends over any given point of the Earth's surface at the same local mean solar time. The surface illumination angle will be nearly the same every time. This consistent lighting is a useful characteristic for satellites that image the Earth's surface in visible or infrared wavelengths (e.g. weather and spy satellites) and for other remote sensing satellites (e.g. those carrying ocean and atmospheric remote sensing instruments that require sunlight). For example, a satellite in sun-synchronous orbit might ascend across the equator twelve times a day each time at approximately 15:00 mean local time. This is achieved by having the osculating orbital plane precess (rotate) approximately one degree each day with respect to the celestial sphere, eastward, to keep pace with the Earth's revolution around the Sun.[1]
The uniformity of Sun angle is achieved by tuning the inclination to the altitude of the orbit (details in section "Technical details") such that the extra mass near the equator causes orbital plane of the spacecraft to precess with the desired rate: the plane of the orbit is not fixed in space relative to the distant stars, but rotates slowly about the Earth's axis. Typical sun-synchronous orbits are about 600–800 km in altitude, with periods in the 96–100 minute range, and inclinations of around 98° (i.e. slightly retrograde compared to the direction of Earth's rotation: 0° represents an equatorial orbit and 90° represents a polar orbit).[1]
Special cases of the sun-synchronous orbit are the noon/midnight orbit, where the local mean solar time of passage for equatorial longitudes is around noon or midnight, and the dawn/dusk orbit, where the local mean solar time of passage for equatorial longitudes is around sunrise or sunset, so that the satellite rides the terminator between day and night. Riding the terminator is useful for active radar satellites as the satellites' solar panels can always see the Sun, without being shadowed by the Earth. It is also useful for some satellites with passive instruments which need to limit the Sun's influence on the measurements, as it is possible to always point the instruments towards the night side of the Earth. The dawn/dusk orbit has been used for solar observing scientific satellites such as Yohkoh, TRACE, Hinode and Proba-2, affording them a nearly continuous view of the Sun.
Sun-synchronous orbits are possible around other oblate planets, such as Mars. But for example Venus is too spherical for having a satellite in sun-synchronous orbit. See for example the article Venus where a flattening coefficient of zero for this planet is cited.
Technical details
Equation (20) of the article Orbital perturbation analysis (spacecraft) gives that the precession rate of an orbit around an oblate planet is
radians per orbit.
As the orbital period of a spacecraft is 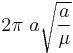 and as
and as 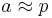 for a circular or almost circular orbit it follows that such an orbit is sun-synchronous if and only if
for a circular or almost circular orbit it follows that such an orbit is sun-synchronous if and only if
where
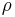 is the mean motion of the Earth in its orbit around the Sun (
is the mean motion of the Earth in its orbit around the Sun (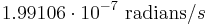 )
)
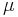 is the gravitational constant of the Earth (
is the gravitational constant of the Earth (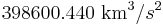 )
)
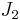 is the coefficient for the second zonal term (
is the coefficient for the second zonal term (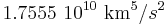 )
)
As an example, for a=7200 km (the spacecraft about 800 km over the Earth surface) one gets with this formula a sun-synchronous inclination of 98.696 deg.
The definition of the Local time of the ascending node concept for Sun-synchronous spacecraft is only related to the position of the Sun indirectly through Newcomb's formula which gives the angle between the Greenwich meridian and the Vernal equinox in the form
where 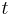 is the time in days from a reference epoch that corresponds to mid-night at the Greenwich meridian and
is the time in days from a reference epoch that corresponds to mid-night at the Greenwich meridian and 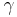 is an extremely small coefficient. Nowadays one uses 2000/01/01 00:00:00 corresponding to Modified Julian Day zero. This then means (counting angles in radians) that the angle from Vernal equinox to the direction away from the Sun projected down to the equatorial plane must be approximately
is an extremely small coefficient. Nowadays one uses 2000/01/01 00:00:00 corresponding to Modified Julian Day zero. This then means (counting angles in radians) that the angle from Vernal equinox to the direction away from the Sun projected down to the equatorial plane must be approximately
The right ascension of the ascending node (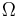 ) for a sun-synchronous orbit increases with precisely this rate
) for a sun-synchronous orbit increases with precisely this rate
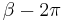 radian/day (
radian/day (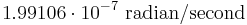 )
)
which is the "mean motion" of the Earth in its orbit around the Sun.
The local time of the ascending node in hours is then the constant value
where 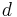 is
is 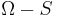 reduced modulo
reduced modulo 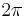 to the interval
to the interval
The local time of the descending node is obtained by adding (or subtracting) 12 hours
The Sun-synchronous orbit is mostly selected for Earth observation satellites that should be operated at a relatively constant altitude suitable for its Earth observation instruments, this altitude typically being between 600 km and 1000 km over the Earth surface. Because of the deviations of the gravitational field of the Earth from that of a homogeneous sphere that are quite significant at such relatively low altitudes a strictly circular orbit is not possible for these satellites. Very often a frozen orbit is therefore selected that is slightly higher over the Southern hemisphere than over the Northern hemisphere. ERS-1, ERS-2 and Envisat of European Space Agency as well as the MetOp spacecraft of the European Organisation for the Exploitation of Meteorological Satellites are all operated in Sun-synchronous, "frozen" orbits.
See also
- Orbital perturbation analysis (spacecraft)
- Analemma
- Geosynchronous orbit
- Geostationary orbit
- List of orbits
- Polar orbit
- World Geodetic System
References
- ^ a b M. Rosengren: ERS-1 - An Earth Observer that exactly follows its Chosen Path, ESA Bulletin number 72, November 1992
- Sandwell, David T., The Gravity Field of the Earth - Part 1 (2002) (p. 8)
- Sun-Synchronous Orbit dictionary entry, from U.S. Centennial of Flight Commission
- NASA Q&A
- Boain, Ronald J. (2004-02). "The A-B-Cs of Sun Synchronous Orbit Design". Space Flight Mechanics Conference. http://trs-new.jpl.nasa.gov/dspace/bitstream/2014/37901/1/04-0327.pdf.